个 人 简 历

教育经历

· 1998-9 - 2002-7 华东师范大学数学系，基础数学，学士学位

· 2004-9 - 2007-7 太阳集团，基础数学，硕士学位

· 2012-9 - 2013-10 日本大阪市立大学数学系，基础数学，博士学位

（教育部海外学位学历认证编号：教留服认日[2013]06777号）

· 2017-9 - 2020-9 汕头大学数学系，基础数学，博士学位

工作经历

· 2002-7 - 2007-12 太阳集团，助教

· 2008-1 - 2013-12 太阳集团，讲师

· 2014-1 - 2023-12 太阳集团，副教授

· 2024-1 – 至今 太阳集团，教授

个人简介

朱剑峰，男，福建晋江籍，太阳集团教授，硕士生导师，2013年10月获得日本大阪市立大学理学博士学位，2020年9月获得汕头大学理学博士学位。多次受邀出访日本、希腊、波兰、黑山共和国等，并作学术报告。具有较好的英语口语能力，2014年取得“suncitygroup太阳集团全英文授课资格”，并承担国际学院的全英文教学，课程包括:《Calculus》、《Linear Algebra》、《Probability and Statistics》。和国内外同行保持密切联系并开展学术合作，研究兴趣包括：拟共形映射、调和映射、函数空间、算子理论等。已发表学术论文30余篇，部分成果发表在“Adv. Math.”、“Math. Ann.”、“J. Funct. Anal.”、“Math. Z.”、“J. Geom. Anal.”等国际著名数学杂志。主持国家自然科学基金面上项目1项，国家青年基金1项，福建省面上项目2项。指导研究生获得“2022年度福建省优秀硕士学位论文”。多个国际期刊特约审稿人，美国数学会评论员，厦门数学会理事。

科研项目

● 主持国家自然科学基金面上项目，45万，关于拟共形映射哈代空间理论和Hölder正则性的研究，执行年限：2023年1月-2026年12月，在研

● 主持国家自然科学基金青年基金项目，21万，关于调和映照的边界特征及其相关问题的研究， 执行年限：2016年1月-2018年12月，已结题

● 主持福建省面上基金项目，4万，几类偏微分方程解的拟共形性质及其算子理论的研究，执行年限：2021年11月-2024年11月，在研

● 主持福建省面上基金项目，3万，调和映照的拟共形延拓及相关的偏差估计，执行年限：2016年4月-2019年4月，已结题

● 参与国家自然科学基金面上项目，48万，复射影空间上调和拟共形映照的若干极值问题，执行年限：2020年1月-2023年12月，在研，排名第二。

近5年发表的论文（节选）

[1] Jinsong Liu and Jian-Feng Zhu*（朱剑峰）, Riesz conjugate functions theorem for harmonic quasiconformal mappings, Adv. Math.434 (2023), Paper No. 109321.

[2] Jinsong Liu，Petar Melentijević, and Jian-Feng Zhu*（朱剑峰）, Lp norm of truncated Riesz transform and an improved dimension-free Lp estimate for maximal Riesz transform, Math. Ann. 2023, DOI:10.1007/s00208-023-02736-1.

[3] David Kalaj, Petar Melentijević, and Jian-Feng Zhu *（朱剑峰）, Lp-theory for Cauchy-transform on the un it disk, J. Funct. Anal. 2022, 282(4): 109337-35 pp

[4] Shaolin Chen*, Hidetaka Hamada, and Jian-Feng Zhu（朱剑峰）, Composition operators on Bloch and Hardy type space, Math. Z. (2022) 301:3939–3957.

[5] Jian-Feng Zhu（朱剑峰）and David Kalaj* ; Norm estimates of the Cauchy transform and related operators, J. Funct. Anal. 2020, 279(9): 108726-25 pp

[6] Jian-Feng Zhu （朱剑峰）, Norm estimates of the partial derivatives for harmonic mappings and harmo nic quasiregular mappings, J. Geom. Anal. 2021, 31(6): 5505-5525.

[7] Sh. Chen and J.-F. Zhu(朱剑峰), Schwarz type lemmas and a Landau-type theorem of some classes of complex-valued functions, Bull. des Sci. Math. 154 (2019), 36-63.

[8] D. Kalaj and J.-F. Zhu(朱剑峰), The existence of minimizers of energy for diffeomorphisms between two-dimensional annuli in

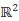and

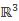, Nonlinear Anal.-Theor. 217 (2022), 112764, 16 pp.

[9] J.-F. Zhu(朱剑峰) and D. Kalaj, Neohookean deformations of annuli in the higher dimensional Euclidean space，Nonlinear Anal.-Theor. 189 (2019), 111575, 14 pp.

[10] J.-F. Zhu(朱剑峰) and A. Rasila,

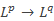norm estimates of Cauchy transforms on the Dirichlet problem and their applications，J. Math. Anal. Appl. 502 (2021), 125255.

[11] J. Huang, A. Rasila and J.-F. Zhu(朱剑峰), Lipschitz property with respect to pseudo-hyperbolic metric for harmonic Bloch mappings, Analysis Mathematica 48 (2022), 1069–1080.

[12] X.-J. Bai, J. Huang, and J.-F. Zhu(朱剑峰), The Schwarz lemma at the boundary for harmonic mappings having zero of order

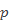, Bull. Malays. Math. Sci. Soc. 44 (2021), 827-838.

[13] Xiao-Jin Bai and J.-F. Zhu(朱剑峰), Norm estimates for a class of operators related to the Bergman projection，Complex Var. Elliptic Equ. 67(2022), 1801–1816.

[14] J.-F. Zhu(朱剑峰), Schwarz-Pick type estimates for gradients of pluriharmonic mappings of the unit ball, Results Math. 74 (2019), 16 pp.

[15] D. Kalaj and J.-F. Zhu(朱剑峰), Schwarz Pick type inequalities for harmonic maps between Riemann surfaces, Complex Var. Elliptic Equ. 64 (2019), 1364-1375.

[16] M. R. Mohapatra, X. Wang, and J.-F. Zhu(朱剑峰), Boundary Schwarz lemma for solutions to nonhomogeneous biharmonic equations, Bull. Australian Math. Soc. 100 (2019), 470-478.

[17] D. Partyka, K. Sakan, and J.-F. Zhu(朱剑峰), Quasiconformal harmonic mappings with the convex holomorphic part, Ann. Acad. Sci. Fenn. Math. 43 (2018), 401-418.

[18] J. Huang and J.-F. Zhu(朱剑峰), Bi-Lipschitz property and distortion theorems for planar harmonic mappings with

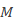-linearly connected holomorphic part, Bull. Korean Math. Soc. 52 (2018), 1419-1431.

[19] X. Wang and J.-F. Zhu(朱剑峰), Boundary Schwarz lemma for solutions to Poisson's equation, J. Math. Anal. Appl. 463 (2018), 623-633.

[20] J.-F. Zhu(朱剑峰), Schwarz lemma and boundary Schwarz lemma for pluriharmonic mappings, Filomat 32 (2018), 5385-5402.

奖 励

● 获2016年度厦门市引进重点人才

● 指导研究生获得“2022年度福建省优秀硕士学位论文”